http://cs231n.github.io/linear-classify/ を参考に一部加筆した。
1. 損失関数
Lesson2では、ピクセルの値からクラススコアを計算する関数を定義した。この関数は重みWでパラメータ化された。さらに、我々はデータ(xi,yi)はコントロールできないがこれらの重み付けは予想された分類スコアが訓練データの真のラベルと整合するようにコントロールできる。

例えば、猫の画像とその“猫”、“犬”、“船”のスコアの例に戻ると、特定の重みが全く適切でないことがわかる。猫の画像であるが、猫のスコアは他のスコアに比べてとても低い。我々は損失関数のようなもので我々の不幸さを結果から測ることにする。直観的に、分類が誤っているときに損失は高く、うまくいっているときに損失は低い。
マルチクラスサポートベクトルマシン損失
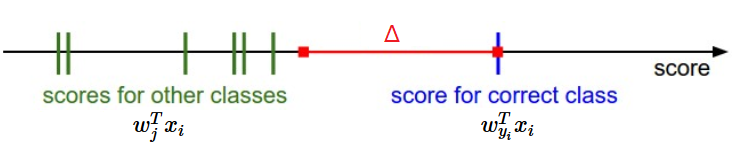
損失関数の定義の方法は複数ある。最初の例として、我々はサポートベクトルマシン(SVM)損失と呼ばれるよく使われる損失を開発する。SVM損失は、SVMが各画像にとって正しい分類が正しくない分類より固定されたマージンΔだけ高いスコアをもつように“望む”ように設定される。このように損失関数にしたようにときどき擬人化するのが役に立つ。SVMは結果がより低い損失になるような特定の結果を“望む”。
i番目の例が画像のピクセルxiと正しい分類を特定するラベルyiを持つ。スコア関数はピクセルを取り分類スコアベクトルf(xi,W)を計算するが、われわれはsと簡素化する。例えば、j番目のスコアはj番目の要素sj=f(xi,W)j。i番目の画像のマルチクラスSVM損失は下式のようになる
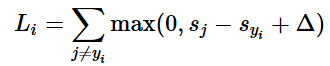
例. 3つの分類がありそのスコアs=[13,−7,11]とし、最初の分類が正しい分類(yi=0)とする。Δは10と仮定する。上式は全ての正しくない(j≠yi)分類を合計するためL
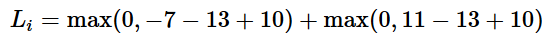
[-7 – 13 + 10]が負であるため最初の項は0であることがわかる。正しい分類のスコア(13)が正しくない分類のスコア(-7)より大きいためこの項は損失0である。さらに言えば、差は20で、10よりだいぶ大きいがSVMは差が少なくとも10であることのみを気にしている。マージン以上のどんな差もmax操作で0に固定される。2つ目の項[11 – 13 + 10]は8になる。正しい分類のスコアが正しくない分類のスコアより大きくてもマージンを超えておらず、このため損失が8となる。まとめると、SVM損失関数は正しい分類yiのスコアが正しくないスコアよりΔだけ大きくなって欲しい。そうでなければ損失を加えることになる。
この特定のモジュールでは線形スコア関数を扱っており、損失関数の等価な式として下のように書き換えることができる。
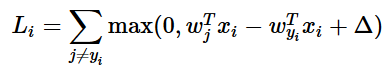
ここでwjはWのj番目の行を列に変形したものである。しかし、これはさらに複雑なスコア関数を扱い始めると必ずしも正しくない。0を閾値としたmax(0,−)はヒンジ損失と呼ばれる。2乗ヒンジ損失SVMを使う人もたまにおり、マージンを超えた値が強調される(線形でなく2次関数的になる)。2乗しないバージョンがより標準的であるが、2乗したものがよりうまくいく場合もある。
正則化(Regularization)
前述した損失関数には1つバグがある。データセットと全ての例を正しく分類するパラメータWがあるとする。問題はこのWが必ずしも一意に決まらないということである。例を正しく分類できるWはたくさんあるかもしれない。正しく分類できるW(つまりそれぞれの例で損失が0)があったら、λW(λ>1)も損失関数が0である。なぜなら、この変形はスコア全体を定数倍し、差も低数倍されるためである。例えば正しいスコアと他のスコアの差が15のとき、全てのWの要素を2倍すると新しい差は30になる。
言い換えると、この曖昧さを無くすために重みWにいくつかの優先度を付与したい。これを損失関数Wに正則化ペナルティR(W)を加えて拡張することで実現する。最も一般的な正則化ペナルティは、すべてのパラメータに対する要素ごとの2次ペナルティによって大きな重みがつきにくいL2ノルムである。
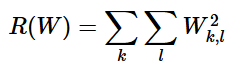
この表現で、Wのすべての要素を2乗し足し合わせている。正則化関数はデータの関数ではないことに留意したい。正則化関数は重みのみを基にしている。正則化ペナルティを含めると完全なSVM損失が求められる。それはデータ損失(損失Liの平均)と正則化損失である。つまり、マルチクラスSVM損失は下記のようになる。
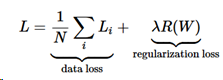
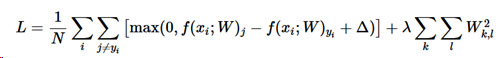
ここでNは訓練データの数である。見てわかるように、正則化ペナルティにパラメータλで重み付けした。このパラメータを簡単に設定する方法はなく、普通はクロスチェックによって決められる。
まとめ
- イメージピクセルから分類スコアを出すスコア関数(この項では重みWとバイアスbに依存する線形関数)を定義した
- k近傍法と違い、パラメータアプローチの利点は学習後に訓練データを捨てることができることである。さらに、全ての訓練データと比較するような浪費をせずに、行列Wと積を1回計算するだけでよいため、テスト画像の分類が速い。
- バイアストリックを導入することで、バイアスベクトルを重みWに入れ込むことができ、1つのパラメータを追いかけるだけで良くなった。
- 訓練データの正しいラベルとパラメータのセットがどれだけ合っているかを定量化できる損失関数を定義した。損失関数において、良い予測をするのと損失が低いのが等価であることを知った。