http://cs231n.github.io/linear-classify/ を参考に一部加筆した。
線形分類器
K近傍法は、訓練画像と分類する画像を比較することで分類する方法で
- 全ての訓練データを全てメモリに記録し、テストデータtの比較のため保持しなければならなかった。
- テストデータの分類には全ての訓練データとの比較が必要であるため、コストがかかる
ここで、畳み込みニューラルネットワーク(CNN)に展開できる強力な分類手法を開発する。そのアプローチは①生データから分類スコアを計算するスコア関数と②予測したスコアと真のスコアとの合致度を定量化する損失関数の2つの要素からなる。線形分類器は損失関数をスコア関数に対して最小化する最適化問題である。
画像からラベルスコアへのパラメータ化マッピング
まず、ある画像のピクセルの値からそれぞれの分類のスコアを計算するスコア関数を定義する。抽象的な例から始める。それぞれがラベルyiと対応する画像の訓練データセットxi∈RDを仮定する。ここで、i=1…N, yi∈1…K, つまり、N個の例があり、それぞれがD次元でK個のカテゴリーに分すりする。例えばCIFER-10のデータセットの場合D=32×32×3色=3072ピクセルでK=10分類(犬、猫、車…)ある。今、スコア関数fをf : RD↦RKと定義する。
線形分類器-ここでは最も簡単な線形写像から始める。
f(xi,W,b)=Wxi+b
上式でxiは画像の全てのピクセルをD×1の1列ベクトルに変換したものである。行列Wは重みと呼ばれ、bはxi無関係に出力スコアに影響を及ぼすためバイアスベクトルと呼ばれる。Wは(K×D)、bは(K×1)の行列である。
ポイント
- 行列の積Wxiは10個(Fig.1の場合3個)の分類を効率よく並列に評価する。ここでそれぞれの分類はWの列に対応する。
- 入力データ(xi,yi)は与えられた固定されたデータとしているが、のW,bパラメータは設定できる。目的は計算されたスコアがすべての訓練データセットに対して正しいラベルとマッチするようにW,bのパラメータを設定することである。直観的に説明すると、正しい分類が正しくない分類より高いスコアを持つようにしたい。
- このアプローチの利点は、訓練データは正しいW,bを求めるために使われるが、一度パラメータを求めれば訓練データは必要なくなることである。このためテストデータの分類は単純に関数を基にスコアを計算していけばよい。
- テスト画像を分類するには1つの行列の積と足し算をすればよく、K近傍法のように全ての訓練画像と比較する必要がない。
Fig.1に2×2ピクセルの画像を例に説明する。2×2の画像(D=4)を4×1の縦長のベクトルに変換する。猫、犬、船の3つに分類(K=3)するため、Wは(3×4)でbは(3×1)の行列になる(行列内の数字は適当な初期値を入れた)。これらの値を用いてf(xi,W,b)計算すると猫、犬、船のそれぞれのスコアが求めらる。

線形分類器を理解する
線形分類器は3色それぞれの全てのピクセルの値に重みづけして合計したスコアを計算する。重み関数は重みづけの値によって画像内の特定の位置にある特定の色が分類のされやすさを決める。例えば、画像の端にたくさん青色があれば(水である可能性が高く)、“船”に分類されやすい。“船”の分類器は青に大きな正の重みづけをし(青色があると船のスコアが上がり)、緑や赤色に負の重みづけをする。
画像を高次元のポイントとみなすアナロジー
画像が高次元の列ベクトルに変換されたため、それぞれの画像をこの空間の1つの点と考えることができる。(たとえばCIFAR-10は1つのポイントは3072-次元空間にいる)。同様に考えて、全てのデータセットは(分類ラベルのついた)点のセットである。
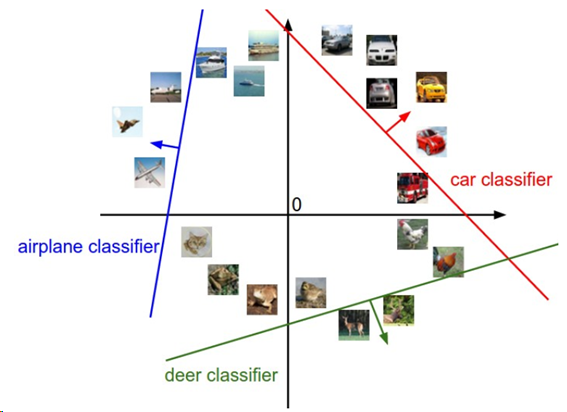
画像スペースのイメージ、それぞれの画像は点であり、3つの分類器(classifier)が表示してある。
上図のようにWの1列1列が1つ1つの分類器である。Wのある列を変えると、図中の対応するラインは違う方向に回転する。バイアスbを変えるとはラインは移動する。特に、バイアスが無い(b=0)とき、xi=0ではスコアは重みに関係なく常にゼロで全てのラインは原点を通る。
線形分類器のテンプレートマッチングとしての理解
Wの別な理解の仕方としてはWのそれぞれの列がそれぞれの分類のテンプレートに対応するという考え方がある。ある画像のそれぞれの分類のスコアは各々のテンプレートと画像を比較することによって得られる。比較には1つ1つのテンプレートと内積をとり、最も”適合”する分類を見つける。”適合”という用語からもわかるように、線形分類器はテンプレートマッチングを行っているが、そのテンプレートは学習により得られたものである。我々はまだ効率的な近傍法を行っているとも考えられる。しかし、数千の訓練データと比較する代わりに、1つの分類あたり1つの画像を使い(学習するが、訓練セットの画像である必要はない)、距離L1あるいはL2の代わりの距離として(負の)内積をとる。

さらに馬のテンプレートは二つの頭を持っているように見えるが、これはデータセットの中に右を向いた馬の写真もあれば左を向いた馬の写真もあるからである。線形分類器はこれらの2つの馬のモードをマージして一つのテンプレートにする。同様に車の分類もいくつかのモードを全ての方向を識別する単一のテンプレートにマージしたように見える。特にこのテンプレートは車体の色が赤で終わっているが、これはCIFER-10のデータセットにほかのどの色よりも赤色の車が多く含まれていたことを示唆する。線形分類器は異なる色を適切に説明するのには向かないが、後で紹介するニューラルネットワークには可能である。ニューラルネットワークは隠れ層に特定の車種(例えば左向きの緑色の車、前向きの青色の車)を検出できる介在ニューロンを開発することができ、次の層のニューロンは個々の車の検出器の重みの合計から、これらをより正確な車のスコアに結合することができる。
バイアストリック
次に進む前にWとbをより簡潔に表現するトリックについて述べる。スコア関数は下記の式で表された。
f(xi,W,b)=Wxi+b
今後計算を進めるのにbとWを別々に扱うのは少し面倒である。よく使われるトリックは2つのパラメータを1つの行列にする。これはxiに常に1になる追加の1次元-デフォルトバイアス次元を拡張することで実現する。追加の次元を用いて、新しいスコア関数は行列の積1つに単純化される。
f(xi,W)=Wxi
下図の例では[4×1]のxiが[5 x 1]になり、Wは[3×4]から [3×5]になり、Wとbが一緒になる。
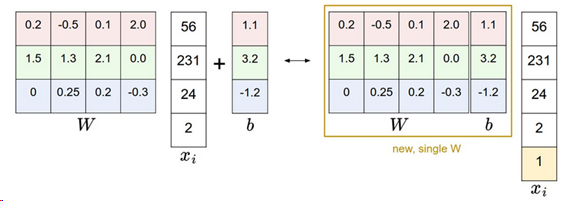
画像データ処理
上の例は生のピクセル値(0-255の範囲の値)を使った。機械学習では、入力特性(画像の場合すべてのピクセルは特性である)を毎回規格化するのが共通した方法である。特に平均を差し引くことでデータを中心値にするのが重要である。画像の場合、この特性は訓練画像全ての平均画像を計算し、画像のピクセルがだいたい[-127~127]の範囲になるように全ての画像から平均画像を引き算する。次の共通の処理はそれぞれの入力特性を値が[-1~1]になるように規格化する。当然、ゼロ平均センタリングは重要であるが、勾配降下法のところで説明する。
損失関数
前のセクションでは、ピクセルの値からクラススコアを計算する関数を定義した。この関数は重みWでパラメータ化された。さらに、我々はデータ(xi,yi)はコントロールできないがこれらの重み付けは予想された分類スコアが訓練データの真のラベルと整合するようにコントロールできる。
例えば、猫の画像とその“猫”、“犬”、“船”のスコアの例に戻ると、特定の重みが全く適切でないことがわかる。猫の画像であるが、猫のスコアは他のスコアに比べてとても低い。我々は損失関数のようなもので我々の不幸さを結果から測ることにする。直観的に、分類が誤っているときに損失は高く、うまくいっているときに損失は低い。
マルチクラスサポートベクトルマシン損失
損失関数の定義の方法は複数ある。最初の例として、我々はサポートベクトルマシン(SVM)損失と呼ばれるよく使われる損失を開発する。SVM損失は、SVMが各画像にとって正しい分類が正しくない分類より固定されたマージンΔだけ高いスコアをもつように“望む”ように設定される。このように損失関数にしたようにときどき擬人化するのが役に立つ。SVMは結果がより低い損失になるような特定の結果を“望む”。
i番目の例が画像のピクセルxiと正しい分類を特定するラベルyiを持つ。スコア関数はピクセルを取り分類スコアベクトルf(xi,W)を計算するが、われわれはsと簡素化する。例えば、j番目のスコアはj番目の要素sj=f(xi,W)j。i番目の画像のマルチクラスSVM損失は下式のようになる
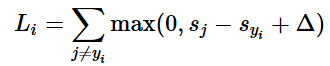
例. 3つの分類がありそのスコアs=[13,−7,11]とし、最初の分類が正しい分類(yi=0)とする。Δは10と仮定する。上式は全ての正しくない(j≠yi)分類を合計するためL
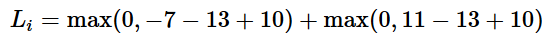
[-7 – 13 + 10]が負であるため最初の項は0であることがわかる。正しい分類のスコア(13)が正しくない分類のスコア(-7)より大きいためこの項は損失0である。さらに言えば、差は20で、10よりだいぶ大きいがSVMは差が少なくとも10であることのみを気にしている。マージン以上のどんな差もmax操作で0に固定される。2つ目の項[11 – 13 + 10]は8になる。正しい分類のスコアが正しくない分類のスコアより大きくてもマージンを超えておらず、このため損失が8となる。まとめると、SVM損失関数は正しい分類yiのスコアが正しくないスコアよりΔだけ大きくなって欲しい。そうでなければ損失を加えることになる。