機械学習 CS231n Lesson2 画像分類と線形分類器

1.画像ファイル

　基本的に画像ファイルは座標（縦×横）と色（Blue, Green, Red）の濃淡で構成される。

　画像＝縦×横×色（B, G, R）

　これはどういうことかをFig1の縦じまの絵を用いて説明します。

縦じまの絵は縦17×横26ピクセルの画像で、下の3つの数値の配列はこの画像を表すデータです。青、緑、赤それぞれ画像と同じ縦17×横26の配列になっております。そして各座標には0~255(8 bit)の濃淡を表す数値が入っています。

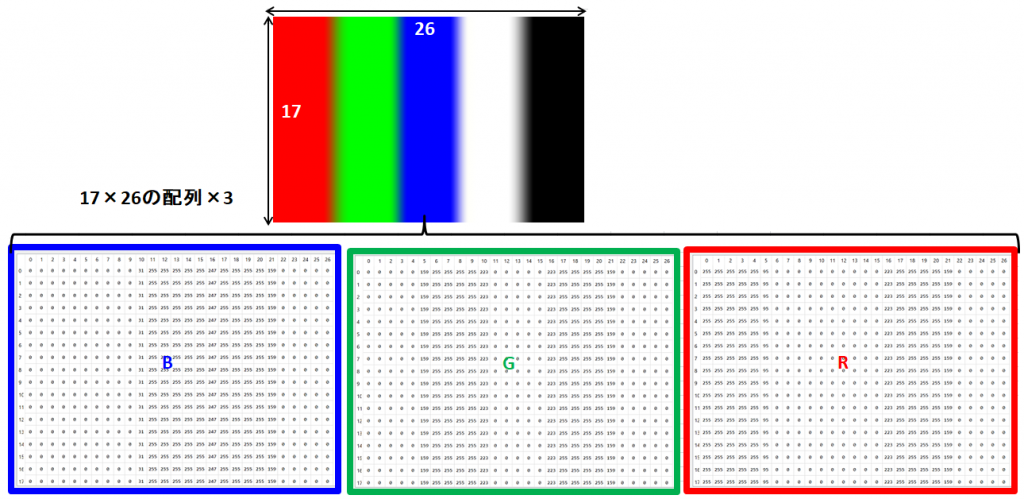
　数値の対応が分かりやすいようにFig1の図を縦に重ねてみました（Fig2）。画像の左が赤になっていることから、赤（R）の配列の横座標0～4が255と最も濃くなっています。緑、青も同様に対応している部分が255になっており、それぞれの境界は色が混ざっているため中間の値になっています。

　また、RGBを足した色であるためRGB全てが255になっており、黒は反対に0になっています。これでなんとなく画像ファイルが分かったような気がします。

2. 画像分類（Image classification）

　画像分類とは例えば人の写真をみて、コンピュータがどの部分が人でどの部分が関係のない背景かを見分けることです。人工知能の世界では画像分類のサンプルデータとしてCIFAR-10が有名です。CIFAR-10は50,000枚＋10,000の画像で10種類のモノ（飛行機、車、鳥、猫など）と正解のラベルがセットになっています。50,000枚が訓練画像で10,000がテスト画像であり、このデータセットでプログラムの精度を比較します。

　代表的な分類法には以下のような方法があります。

• K-Nearest Neighbor（K近傍法）
• Linear classifiers: SVM, Softmax（線形分類器）
• Neural network（ニューラルネットワーク）

3.K近傍法

　K近傍法は正答率が低いが、シンプルで理解しやすい方法であるため機械学習の導入として良いらしい。K近傍法はテスト画像I1と訓練画像I2の距離dを計算し最も距離が近いK個の多数決で分類を決める方法。距離は単に差分の絶対値を求めるものと、２乗和のルートをとるものがある。

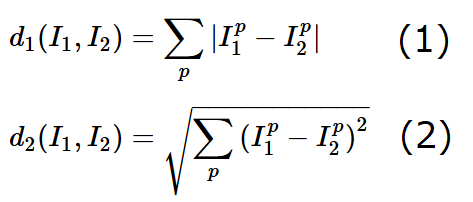
　pはピクセルを表す。以下Fig.3を使ってd1を例に距離の求め方を説明する。

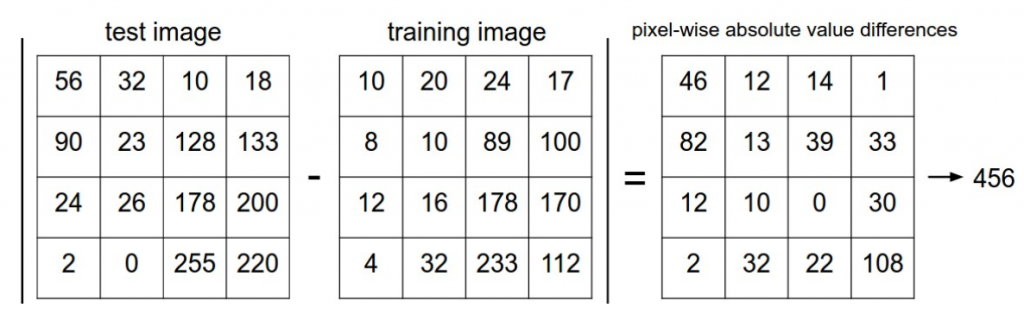
Fig.1は画像の4×4ピクセルのデータを示しており、テスト画像、訓練画像、（テスト画像）‐（訓練画像）の計算結果の順に並んでいる。式（１）のI1p(p=1, 2…16)は各ピクセルのことを表しているため、例えばI11は左上のピクセルで56、I14は右上のピクセルで18となる。d1の式は各ピクセルで差分をとって合計するという意味なので3番目の差分の結果の合計を取り456となる。

　例えばK=5で100個の訓練データがあった場合、この100個の訓練画像とテスト画像の差分をとる。距離が最も小さい5個が例えば（猫、飛行機、車、猫、犬）であればこのテスト画像の分類は”猫”となる。尚、最適なKの値の選び方は問題によって変わるため、トライアンドエラーで見つけるしかないらしい。K近傍法は分類のたびに訓練データと距離をとるため効率の悪いアルゴリズムである。

線形分類器

http://cs231n.github.io/linear-classify/ を参考に一部加筆した。

K近傍法は、訓練画像と分類する画像を比較することで分類する方法で

• 全ての訓練データを全てメモリに記録し、テストデータｔの比較のため保持しなければならなかった。
• テストデータの分類には全ての訓練データとの比較が必要であるため、コストがかかる

ここで、畳み込みニューラルネットワーク（CNN）に展開できる強力な分類手法を開発する。そのアプローチは①生データから分類スコアを計算するスコア関数と②予測したスコアと真のスコアとの合致度を定量化する損失関数の2つの要素からなる。線形分類器は損失関数をスコア関数に対して最小化する最適化問題である。

画像からラベルスコアへのパラメータ化マッピング

まず、ある画像のピクセルの値からそれぞれの分類のスコアを計算するスコア関数を定義する。抽象的な例から始める。それぞれがラベルyiと対応する画像の訓練データセットxi∈RDを仮定する。ここで、i=1…N,  yi∈1…K, つまり、N個の例があり、それぞれがD次元でK個のカテゴリーに分すりする。例えばCIFER-10のデータセットの場合D=32×32×3色=3072ピクセルでK=10分類（犬、猫、車…）ある。今、スコア関数fをf : RD↦RKと定義する。

線形分類器－ここでは最も簡単な線形写像から始める。

f(xi,W,b)=Wxi+b

上式でxiは画像の全てのピクセルをD×1の１列ベクトルに変換したものである。行列Wは重みと呼ばれ、bはxi無関係に出力スコアに影響を及ぼすためバイアスベクトルと呼ばれる。Wは（K×D）、bは(K×1)の行列である。

ポイント

• 行列の積Wxiは10個（Fig.1の場合３個）の分類を効率よく並列に評価する。ここでそれぞれの分類はWの列に対応する。
• 入力データ(xi,yi)は与えられた固定されたデータとしているが、のW,bパラメータは設定できる。目的は計算されたスコアがすべての訓練データセットに対して正しいラベルとマッチするようにW,bのパラメータを設定することである。直観的に説明すると、正しい分類が正しくない分類より高いスコアを持つようにしたい。
• このアプローチの利点は、訓練データは正しいW,bを求めるために使われるが、一度パラメータを求めれば訓練データは必要なくなることである。このためテストデータの分類は単純に関数を基にスコアを計算していけばよい。
• テスト画像を分類するには１つの行列の積と足し算をすればよく、K近傍法のように全ての訓練画像と比較する必要がない。

Fig.1に2×2ピクセルの画像を例に説明する。2×2の画像(D=4)を4×1の縦長のベクトルに変換する。猫、犬、船の3つに分類(K=3)するため、Wは(3×4)でbは(3×1)の行列になる（行列内の数字は適当な初期値を入れた）。これらの値を用いてf(xi,W,b)計算すると猫、犬、船のそれぞれのスコアが求めらる。

線形分類器を理解する

線形分類器は3色それぞれの全てのピクセルの値に重みづけして合計したスコアを計算する。重み関数は重みづけの値によって画像内の特定の位置にある特定の色が分類のされやすさを決める。例えば、画像の端にたくさん青色があれば（水である可能性が高く）、“船”に分類されやすい。“船”の分類器は青に大きな正の重みづけをし（青色があると船のスコアが上がり）、緑や赤色に負の重みづけをする。

画像を高次元のポイントとみなすアナロジー

画像が高次元の列ベクトルに変換されたため、それぞれの画像をこの空間の1つの点と考えることができる。（たとえばCIFAR-10は1つのポイントは3072-次元空間にいる）。同様に考えて、全てのデータセットは（分類ラベルのついた）点のセットである。

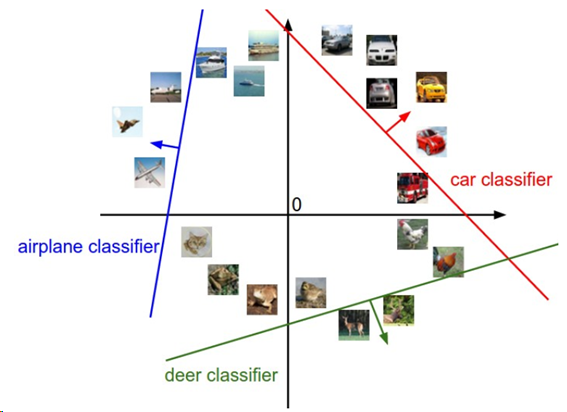
画像スペースのイメージ、それぞれの画像は点であり、3つの分類器（classifier）が表示してある。

上図のようにWの1列1列が１つ１つの分類器である。Wのある列を変えると、図中の対応するラインは違う方向に回転する。バイアスbを変えるとはラインは移動する。特に、バイアスが無い（b=0）とき、xi=0ではスコアは重みに関係なく常にゼロで全てのラインは原点を通る。

線形分類器のテンプレートマッチングとしての理解

Wの別な理解の仕方としてはWのそれぞれの列がそれぞれの分類のテンプレートに対応するという考え方がある。ある画像のそれぞれの分類のスコアは各々のテンプレートと画像を比較することによって得られる。比較には１つ１つのテンプレートと内積をとり、最も”適合”する分類を見つける。”適合”という用語からもわかるように、線形分類器はテンプレートマッチングを行っているが、そのテンプレートは学習により得られたものである。我々はまだ効率的な近傍法を行っているとも考えられる。しかし、数千の訓練データと比較する代わりに、１つの分類あたり１つの画像を使い（学習するが、訓練セットの画像である必要はない）、距離L1あるいはL2の代わりの距離として（負の）内積をとる。

さらに馬のテンプレートは二つの頭を持っているように見えるが、これはデータセットの中に右を向いた馬の写真もあれば左を向いた馬の写真もあるからである。線形分類器はこれらの2つの馬のモードをマージして一つのテンプレートにする。同様に車の分類もいくつかのモードを全ての方向を識別する単一のテンプレートにマージしたように見える。特にこのテンプレートは車体の色が赤で終わっているが、これはCIFER-10のデータセットにほかのどの色よりも赤色の車が多く含まれていたことを示唆する。線形分類器は異なる色を適切に説明するのには向かないが、後で紹介するニューラルネットワークには可能である。ニューラルネットワークは隠れ層に特定の車種（例えば左向きの緑色の車、前向きの青色の車）を検出できる介在ニューロンを開発することができ、次の層のニューロンは個々の車の検出器の重みの合計から、これらをより正確な車のスコアに結合することができる。

バイアストリック

次に進む前にWとbをより簡潔に表現するトリックについて述べる。スコア関数は下記の式で表された。

f(xi,W,b)=Wxi+b

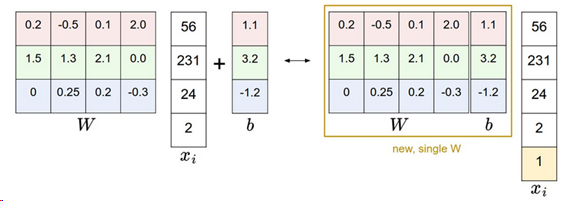
今後計算を進めるのにbとWを別々に扱うのは少し面倒である。よく使われるトリックは２つのパラメータを１つの行列にする。これはxiに常に1になる追加の1次元－デフォルトバイアス次元を拡張することで実現する。追加の次元を用いて、新しいスコア関数は行列の積１つに単純化される。

f(xi,W)=Wxi

下図の例では[4×1]のxiが[5 x 1]になり、Wは[3×4]から [3×5]になり、Wとbが一緒になる。

画像データ処理

上の例は生のピクセル値（0-255の範囲の値）を使った。機械学習では、入力特性（画像の場合すべてのピクセルは特性である）を毎回規格化するのが共通した方法である。特に平均を差し引くことでデータを中心値にするのが重要である。画像の場合、この特性は訓練画像全ての平均画像を計算し、画像のピクセルがだいたい[-127~127]の範囲になるように全ての画像から平均画像を引き算する。次の共通の処理はそれぞれの入力特性を値が[-1~1]になるように規格化する。当然、ゼロ平均センタリングは重要であるが、勾配降下法のところで説明する。